-
- Downloads
Add documentation for basic of PE
- docs/basics-of-parameter-estimation.txt 113 additions, 0 deletionsdocs/basics-of-parameter-estimation.txt
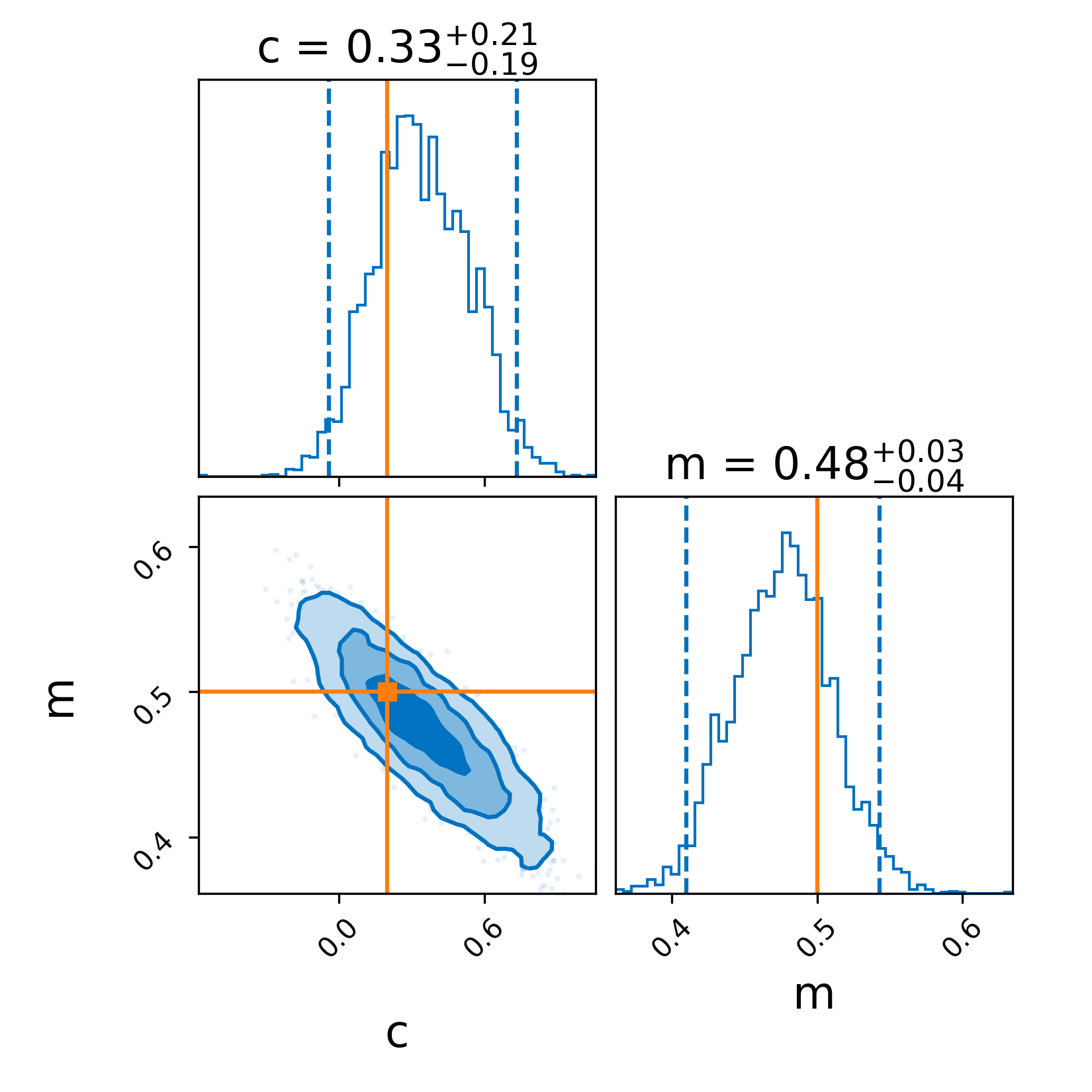
- docs/images/linear-regression_corner.png 0 additions, 0 deletionsdocs/images/linear-regression_corner.png
- docs/images/linear-regression_data.png 0 additions, 0 deletionsdocs/images/linear-regression_data.png
- docs/index.txt 1 addition, 0 deletionsdocs/index.txt
- examples/other_examples/linear_regression.py 1 addition, 1 deletionexamples/other_examples/linear_regression.py
110 KiB
22.2 KiB